Materi Aljabar Linier dan Matriks Lengkap

Posted by : Muhammad Khotibul Umam Sabtu, 28 Desember 2019

Dosen: Pak Hermanto, M. Kom

Materi Aljabar Linier dan Matriks Lengkap

Aljabar Linier dan Matriks

Assalammualaikum wr. wb., Salam sejahtera untuk kita semua semoga apa yang dibaca dan dipelajari dapat membuahkan suatu hasil yang nantinya akan berguna untuk bangsa, amin. Materi ini saya dapatkan dari dosen Aljabar Linier yaitu Ibu Mia Mayang Sari, S.Kom. Dalam artikel ini ada beberapa silabus yang akan dibahas dalam ruang lingkup aljabar linier dan matriks, diantaranya adalah sebagai berikut :

Aljabar Linier Dalam Bidang Informatika

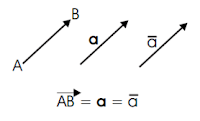
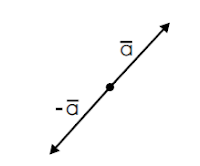
Basis dan Ruang Vektor

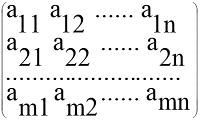
Matriks dan Determinan

Sistem Persamaan Linear

Konsep Nilai Eigen dan Vektor Eigen

Matlab

ALJABAR LINIER DAN MATRIKS DALAM BIDANG INFORMATIKA

Definisi / Pegnertian Aljabar Linier dan Matriks

Aljabar linier adalah bidang studi yang mempelajari sistem persamaan linier dan solusinya, vektor serta transformasi linier.

Matriks adalah kumpulan bilangan, simbol atau ekspresi berbentuk persegi panjang yang disusun menurut baris dan kolom.

Aljabar linier dan matriks merupakan bagian yang sangat berkaitan, matriks merupakan operasi dalam pencarian persamaan aljabar linier.

Contoh Persamaan Linier :

x + y = 4 (persamaan linier dengan 2 peubah)

2x-3y=2z+1 (persamaan linier dengan 3 peubah)

Aljabar Linier dalam Bidang Informatika

Kriptografi : penggunaan teknik matriks identitas

Komputer Grafik : penggunaan teknik matriks transpose

Games : penggunaan berbagai macam teknik matriks

Pengolahan Citra : penggunaan teknik matriks dan persamaan linier

BASIS RUANG DAN VEKTOR

Definisi / Pengertian Basis

Basis adalah himpunan vektor.

Basis juga bisa dianggap sebagai sistem koordinat.

Misalkan V ruang vektor dan S = { s 1, s 2 ,…, s n }. S disebut basis dari V.

Vektor Basis di Ruang R2

Vektor basis diruang R2 pada sumbu X dinyatakan dengan i, vektor satuan pada sumbu Y dinyatakan dengan j

Bentuk vektor baris ditulis sebagai berikut : e1 = (1,0), e2 = (0,1)

Vektor Basis di Ruang R3

Vektor basis diruang R3 pada sumbu X dinyatakan dengan i, pada sumbu Y dinyatakan dengan j, sedangkan vektor satuan pada sumbu Z dinyatakan dengan k.

Bentuk vektor baris ditulis sebagai berikut : e1 = (1,0,0), e2 = (0,1,0), e3 = (0,0,1)

Vektor di Ruang R2

Vektor terletak sepanjang sumbu koordinat X dan Y.

Vektor berada di R2 maka dikatakan vektor berada di bidang.

Vektor di Ruang R3

Vektor dalam ruang digambarkan dalam sistem koordinat ruang.

Sumbu X dan Y mendatar sedangkan sumbu Z vertikal.

Ketiga sumbu tersebut saling tegak lurus dan perpotongan dititik pangkal O (0,0,0).

Pengantar Vektor

Didalam Fisika dikenal 2 buah besaran, yaitu besaran skalar dan besaran vektor.

Skalar adalah besaran yang hanya memiliki nilai.

Contoh skalar : massa.

Vektor didefinisikan sebagai sebuah besaran yang memiliki nilai dan arah.

Contoh vektor : Kecepatan.

Notasi Vektor

Vektor merupakan garis berarah yang memiliki titik awal dan titik akhir.

Arah panah menunjukan arah vektor dan panjang vektor menunjukan besaran vektor.

Vektor dapat ditulis dengan huruf kecil tebal atau tanda bar.

Gambar Vektor

Gambar Vektor

Titik pangkal di A

Titik ujung di B

Arah vektor di A menuju B

Besar vektor ditunjukan oleh panjang garis AB

Operasi-operasi Pada Vektor

Kesamaan dua vektor

Negatif sebuah vektor

Resultan 2 buah vektor

Penjumlahan vektor

Perkalian vektor dengan skalar

Kesamaan Dua Vektor

Suatu vektor dikatakan sama apabila memiliki panjang dan arah yang sama, dengan tidak memperhatikan titik pangkal.

Gambar Kesamaan Dua Vektor

Negatif Sebuah Vektor

Vektor (-a) adalah vektor yang memiliki arah berlawanan dengan vektor a tetapi panjangnya sama dengan vektor a.

Gambar Negatif Sebuah Vektor

Resultan 2 Buah Vektor

Resultan dua vektor u dan v adalah vektor w yang dibentuk dengan menempatkan titik pangkal vektor v pada titik ujung vektor v dan menghubungkan titik pangkal vektor u dengan titik ujung vektor v

Gambar Resultan 2 Buah Vektor

Penjumlahan Vektor

Diketahui a dan b vektor–vektor di ruang yang komponen – komponennya adalah

a = ( a1,a2,a3 ) dan b = ( b1,b2,b3 )

Maka :

a + b = (a1 +b1, a2+b2, a3+b3 )

Contoh :

diketahui dua vektor a = i+2j-3k dan b = 2i+5j+4k, berapakah a+b ?

Perkalian Vektor dengan Skalar Aljabar Linier dan Matriks

Diketahui a vektor di ruang yang komponen – komponennya adalah a = ( a1,a2,a3 )

Maka k . a = ( ka1, ka2, ka3 )

Jika k > 0 maka searah dengan a

Jika k < 0 maka berlawanan arah dengan a

Contoh :

diketahui vektor a = i+2j-3k, maka 2a = ?

Panjang Vektor

Panjang sebuah vektor u disebut juga norma u dinyatakan dengan :

Contoh : hitunglah panjang vektor u = 3i+4j!

Jarak Euclidean Antara Dua Vektor

Jika p = (p1, p2,….pn) dan q = (q1, q2,…qn)

Contoh : diketahui p = (2i+3j) dan q = (5i + 6j), berapa jarak Euclideannya?

Contoh Penerapan Vektor dalam Klasifikasi Citra

Diketahui tiga buah wajah, yaitu Citra 1(Dilla), Citra 2 (Agil), dan Citra 3 (Alim)yang akan digunakan sebagai basis data untuk pengenalan pola wajah menggunakan komputer.

Beberap ciri untuk mengenali citra tersebut adalah dilihat dari standar deviasi intensitas warna dalam tiap-tiap citra σ, rata-ratanya µ, dan entropinya ℯ. Setelah ketiga ciri tersebut dihitung diperoleh data berikut:

Citra 1: σ=0,15 µ=40 ℯ=1,25

Citra 2: σ=0,05 µ=60 ℯ=2,35

Citra 3: σ=0,24 µ=53 ℯ=0,85

Kemudian diambil satu citra lagi, yaitu citra ke-4 sebagai citra uji.

Pada citra uji dihitung nilai-nilai ciri citra tersebut,diperoleh data berikut:

Citra 4: σ=0,23 µ=55 ℯ=0,82

Tentukan bagaimana komputer bisa mengenali citra ke-4?Dan siapakah nama dari citra ke-4 menurut hasil pengenalan komputer?

MATRIKS

Definisi / Pengertian Matriks

Matriks adalah sekumpulan bilangan yang disusun dalam sebuah empat persegi panjang, secara teratur, di dalam baris-baris dan kolom-kolom.

Gambar Matriks

Matriks di atas disebut matriks ukuran m x n

Operasi-operasi pada Matriks

1. Kesamaan Dua Buah Matriks

Dua matriks A dan B disebut sama, jika ukurannya sama dan berlaku : [ aij ] = [ bij ]

A = B

A ≠ C

B ≠ C

2. Penjumlahan dua matriks

Jumlah dua buah matriks A + B bisa dilakukan asalkan kedua matriks tersebut berukuran sama

Sifat-sifat penjumlahan:

Komutatif : A + B = B + A

Assosiatif : A + (B + C) = (A + B) + C

3. Perkalian Matriks dengan Skalar

Jika k suatu skalar, maka matriks kA = (kaij)

Diperoleh dengan mengalikan semua elemen matriks A dengan k

4. Pengurangan Matriks

Mengurangi matriks A dengan B (A-B) adalah menjumlahkan matriks A dengan matriks (-B)

5. Perkalian Matriks

Syarat perkalian matriks : banyaknya kolom matriks pertama = banyaknya baris matriks kedua.

Hasil perkalian antara matriks A = [aij] berordo mxp, dengan matriks B = [bij] berordo pxn, adalah matriks C = [Cij] berordo mxn.

MACAM-MACAM MATRIKS

1. Matriks Bujursangkar Aljabar Linier dan Matriks

Matriks bujursangkar adalah matriks dimana banyaknya baris = banyaknya kolom

Gambar Matriks Bujur Sangkar

2. Matrik Satuan / Identitas

Matriks bujursangkar

Setiap unsurnya nol, kecuali didiagonal utama = 1

Contoh :

Gambar Matrik satuan/ matriks identitas

3. Matriks Segitiga

Matriks bujursangkar

Unsur di atas/di bawah diagonal utama adalah nol

Contoh :

Gambar Matriks Segitiga

4. Matriks Tranpose

Tidak perlu bujursangkar

Setiap baris ditukar tempat dengan kolom

contoh :

Gambar Matriks Tranpose

5. Matriks Diagonal

Matriks bujursangkar

Semua unsur nol, kecuali didiagonal utama

Contoh :

Gambar Matriks Diagonal

6. Aljabar Linier dan Matriks Nol

Tidak perlu matriks bujur sangkar

Semua unsurnya nol

Contoh :

Gambar Matriks Nol

source : https://www.susantokun.com/materi-aljabar-linier-dan-matriks-lengkap/

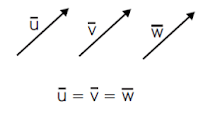
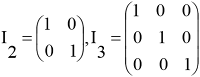
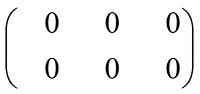
Posting Komentar

- Copyright © Muhammad Khotib Al- Umam - Date A Live - Powered by This Site - Designed by - Shin07